一,问题描述
在Shakespeare文集(有很多文档Document)中,寻找哪个文档包含了单词“Brutus”和"Caesar",且不包含"Calpurnia"。这其实是一个查询操作(Boolean Queries)。
在Unix中有个工具grep,它能线性扫描一篇文档,然后找出某个单词是否在该文档中。因此,寻找哪篇文档包含了“Brutus”和“Caesar”可以用grep来实现。但是:不包含“Calpurnia”如何实现呢?
有时,还有一些更加复杂的情况:比如寻找“Romans”附近出现“countrymen”的文档有哪些?附近 表示寻找的范围,比如在某篇文档中“Romans”和“countrymen”出现在同一段落中,那么这篇文档就是要找的文档;再比如:“Romans”前后10个词内出现“countrymen”,则这篇文档就是要找的文档。这种情况又如何处理?
再比如,寻找 包含单词“Brutus”和"Caesar"的文档,返回的结果有很多篇文档,哪篇文档最相关呢?(Rank retrieval)。这些复杂的情况都无法用 grep 工具来实现,而是使用了一些特殊的数据结构(文档表示方式)。比如 Term-document incidence matrices 和 倒排索引(Inverted index)
二,Term-document incidence matrices
介绍一个新概念:Term
在处理文档时,经常以单词(word)作为分析处理单元(units),但有一些"专有名词",又不是传统意义上的单词,比如"Hong Kong"或者一些一连串的数字。因此,在IR中,用term来表示"index units"。看到这里,就明白tf-idf(term frequency–inverse document frequency) 中的 term 是什么意思了。
Terms are the indexed units,they are usually words, and for the moment you can think of them as words, but the information retrieval literature normally speaks of terms because some of them, such as perhaps I-9 or Hong Kong are not usually thought of as words.
回到文章开头提出的那个问题:哪个文档包含了单词“Brutus”和"Caesar",且不包含"Calpurnia"?,更专业地:
哪个文档包含了 term "Brutus" 和 term "Caesar",且不包含term "Calpurnia"?
首先将文档"拆分"成一个个的 term 来表示,若某个term在这篇文档中出现 就用1标识;未出现则用0标识。

如上图所示:每一列代表一篇文档是否包含了某个term,比如 文档 Julius Caesar 就包含了"Antony"、"Brutus"、"Caesar"、"Calpurnia",但是不包含"Cleopatra"、"mercy"、"worser"。
每一行表示 某个term 出现在哪几篇文档中。比如 term "Antony"出现在第一篇文档、第二篇文档(Julius Caesar)和最后一篇文档中。
有了这个矩阵,就可以回答上面那个问题了。Brutus 在文档中出现情况是 110100;Caesar在文档中出现情况是 110111 ;Calpurnia 出现情况是 101111,将它们进行 与操作:
110100 AND 110111 AND 101111 = 100100
得出:包含了单词“Brutus”和"Caesar",且不包含"Calpurnia"的文档是第一篇文档Antony and Cleopatra 和 第四篇文档 Hamlet。而且对于计算机而言,进行与操作是很快的。
从上面可看出,通过Term-document incidence matrices这种文档的表示形式,将 grep 线性查找操作,变成了 位与 操作。
但是,这种表示方式也存在着问题:这个矩阵会很稀疏。比如中文汉字有几万个(term 很多),一篇新闻文档不会用到所有的中文汉字,因此矩阵中大部分元素为0。而要存储一个很大的稀疏矩阵,对内存就造成了浪费。而倒排索引就可以解决这个问题。
三,inverted index
倒排索引就是:如果某个term在文档中出现了,才记录它。若不出现,则不记录。
A much better representation is to record only the things that do occur, that is, the 1 positions. We keep a dictionary of terms Then for each term, we have a list that records which documents the term occurs in. Each item in the list – which records that a term appeared in a document– is conventionally called a posting
假设有很多文档,如何构建倒排索引呢?首先是从文档中选取出 term,也就是对文档进行分词,得到一个个的 term。比如有N篇文档如下:
文档一: Friends, Romans, countrymen.文档二: So let it be with Caesar .... .... 文档N:
对文档文档分词(tokenize),得到一系列的tokens:Friends、Romans、countrymen、So……
有时还需要对分词的结果进行预处理(linguistic preprocessing),这种预处理操作一般是:删除一些 stop words,进行 Stemming 操作 和 lemmatization操作。stemming操作 是从词形上对单词归一化,比如说:复数cats 变成 cat。而 lemmatization 是寻找词根,比如:are, is, am 都归一化成 be
Stemming usually refers to a crude heuristic process that chops off the ends of words in the hope of achieving this goal correctly most of the time, and often includes the removal of derivational affixes
Lemmatization usually refers to doing things properly with the use of a vocabulary and morphological analysis of words normally aiming to remove inflectional endings only and to return the base or dictionary form of a word, which is known as the lemma。
预处理之后,得到一个个的 可索引的 term 了。倒排索引如下图所示:
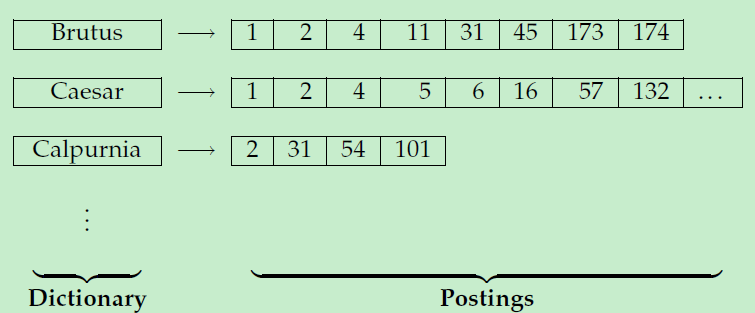
"Brutus"就是一个term,它关联着一个链表(list),这个链表称之为posting,链表中的每个元素代表文档的标识,它表示: term "Brutus"出现在 文档1,文档2,文档4,文档11,文档31……文档174中
若干个 term 组合起来就是一个 dictionary,所有的posting的集合就是 postings
从上可看出,使用倒排索引表示时:每个文档都有一个唯一的文档标识(docID),而且链表是有序的。并且上面的倒排索引只关注:某个term是文档中 是否 出现过,并不知道出现了多少次。
现在如何根据倒排索引找出:哪个文档包含了单词“Brutus”和"Caesar",且不包含"Calpurnia"?这其实就是 "Brutus" 指向的链表 和 "Caesar"指向的链表 求并 操作(intersection)---。算法的伪代码如下:
INTERSECT(p1, p2) answer ← <> while p1 != NIL and p2 != NIL do if docID(p1) = docID(p2) then ADD(answer, docID(p1)) p1 ← next(p1) p2 ← next(p2) else if docID(p1) < docID(p2) then p1 ← next(p1) else p2 ← next(p2) return answer
时间复杂度为:O(N),N就是 文档的总个数。对于两个有序链表 求并 操作,时间复杂度会不会小于O(N)呢?那也是有可能的,那就是在链表的某些元素上,存储一个"skip pointer"指针,如下图所示:
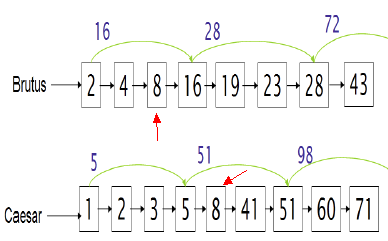
举个例子:假设目前已经找到了两个链表中的第一个公共元素8,现在要找下一个公共元素。链表1移动到下一个位置指向16,链表2移动到下一个位置指向41。由于元素16存储了一个skip pointer,该skip pointer指向28,由于链表是有序的而且28小于41,因此链表1可以直接跳过19、23这两个元素,直接移动到28这个元素上(从而不需要将 19和23 这两个元素与 链表2中的41比较)。算法伪代码如下:
INTERSECTWITHSKIPS(p1, p2)1 answer ← <>2 while p1 != NIL and p2 != NIL3 do if docID(p1) = docID(p2)4 then ADD(answer, docID(p1))5 p1 ← next(p1)6 p2 ← next(p2)7 else if docID(p1) < docID(p2)8 then if hasSkip(p1) and (docID(skip(p1)) ≤ docID(p2))9 then while hasSkip(p1) and (docID(skip(p1)) ≤ docID(p2))10 do p1 ← skip(p1)11 else p1 ← next(p1)12 else if hasSkip(p2) and (docID(skip(p2)) ≤ docID(p1))13 then while hasSkip(p2) and (docID(skip(p2)) ≤ docID(p1))14 do p2 ← skip(p2)15 else p2 ← next(p2)16 return answer
引入skip pointers到底是好还是坏呢?这个不一而足。说几个需要考虑的因素:
①引入skip pointer 需要额外的存储空间。②移动到某个元素上时,需要判断该元素是否存储了 skip pointers。③在哪些元素上存储 skip pointer比较好? skip pointers 跳过多少个元素比较好?……
额外的一点 补充,上面讲到:每个 term 的posting list 长度是未知的。要找某两个term的公共元素,其实就里线性遍历这两个term对应的posting list。因此,这个过程的时间复杂度是O(M+N) 。这里的M是第一个term对应的posting list的长度,N是第二个term对应的posting list的长度。那如果我要找多个term的posting list中的公共元素呢?
比如说:寻找 term : Brutus 、Calpurnia、Caesar这三个term,都在哪些文档中出现了?
这是一个与操作。如果知道 posting list的长度,先将长度比较短的term的posting list进行与操作,这样能提高查询的效率。比如说从上面图中可看出:Calpurnia 的posting list的长度为4,先执行 Calpurnia & Brutus 得出的结果的长度也不会超过4,然后再去Caesar对应的posting list中查询。效率要好。
即:执行顺序为Calpurnia & Brutus & Caesar 比 Caesar & Brutus & Calpurnia 要好。
四,参考资料:
《An Introduction to Information Retrieval》第一章和第二章
原文:http://www.cnblogs.com/hapjin/p/8214254.html